Het verhaal van Plaatswaarde: Hoe ik getallen hun kracht gaf
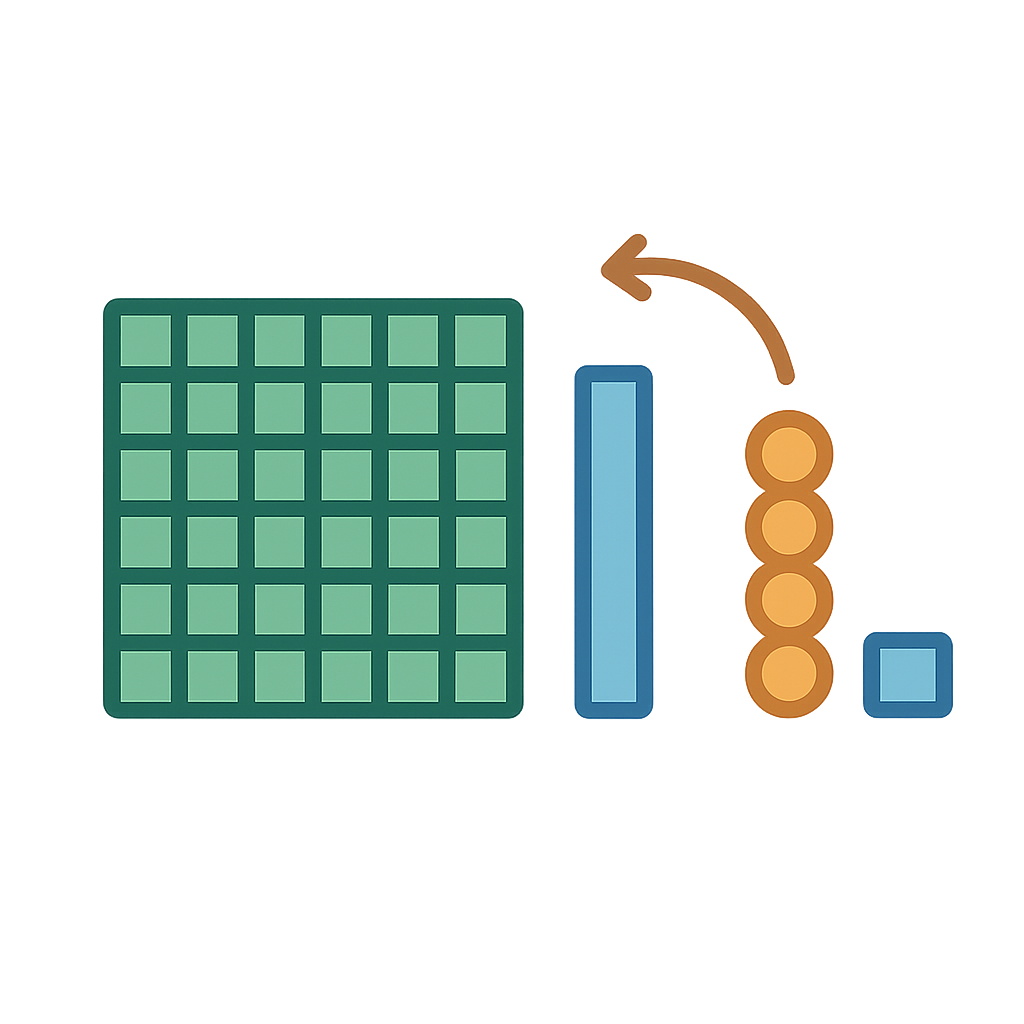
Heb je je ooit afgevraagd wat het verschil is tussen negen en tien? Of negenennegentig en honderd? Het lijkt zo simpel. Je voegt maar één klein dingetje toe, maar plotseling verandert alles. Een getal met één cijfer wordt een getal met twee cijfers. Een getal met twee cijfers wordt een gigantisch getal met drie cijfers. Hoe kan dat? Hoe kan één enkel cijfer, de '1', de ene keer gewoon 'één' betekenen en de andere keer 'honderd'? Dat komt door mij. Ik ben de geheime kracht die cijfers hun waarde geeft op basis van waar ze staan. Ik ben de reden dat de '1' in 100 honderd keer machtiger is dan de '1' in je broekzak. Ik ben de onzichtbare architect van getallen, de stille regel die eenvoudige symbolen omzet in reusachtige hoeveelheden of minuscule breuken. Ik ben de kracht die orde schept in de chaos van het tellen. Mijn naam is Plaatswaarde.
Stel je een wereld voor zonder mij. Een wereld vol onhandige getallen. In het oude Rome was rekenen een ware hoofdpijn. Probeer maar eens CXXIII te vermenigvuldigen met XLVII. Hun cijfers waren als letters die je gewoon bij elkaar optelde, zonder een slim systeem voor de positie. Een 'X' was altijd tien, waar het ook stond. Dit maakte grote berekeningen ontzettend ingewikkeld en het leidde vaak tot fouten. Stel je voor dat je een brug bouwt en je berekening is een beetje fout. Dat is geen goed nieuws. Duizenden jaren geleden, zo'n 4000 jaar geleden in het oude Babylonië, hadden ze al een slimmer idee. Ze waren briljante astronomen en wiskundigen en ze begrepen dat de positie van een symbool ertoe deed. Ze gebruikten een zestigtallig stelsel, wat betekent dat ze met groepen van zestig werkten in plaats van tien. Ze lieten zelfs een open ruimte achter om te laten zien dat een positie leeg was, maar dat was verwarrend. Was die lege ruimte een bewuste lege plek, of had de schrijver gewoon een fout gemaakt? Het was als het lezen van een zin zonder spaties of leestekens. Het werkte een beetje, maar het was rommelig en onbetrouwbaar voor echt complexe wiskunde. De wereld had een betere manier nodig om met getallen om te gaan, een held die de lege plekken kon opvullen en duidelijkheid kon scheppen.
Die held kwam uit India. Daar, rond de 7e eeuw na Christus, waren briljante wiskundigen bezig met een revolutionair idee. Een geleerde genaamd Brahmagupta was een van de eersten die duidelijke regels opschreef voor een heel speciaal nieuw getal: nul. Voorheen was nul slechts een lege ruimte, een afwezigheid. Maar Brahmagupta en zijn tijdgenoten behandelden het als een echt getal, een held met zijn eigen krachten. Met mijn nieuwe vriend Nul kon ik eindelijk mijn ware potentieel laten zien. Het getal '101' was nu duidelijk anders dan '11', omdat Nul de plek van de tientallen kon vasthouden en kon laten zien dat er geen waren. Dit nieuwe systeem, dat we nu de Hindoe-Arabische cijfers noemen, was elegant, efficiënt en ongelooflijk krachtig. Dit geniale idee bleef niet in India. Via handelsroutes zoals de Zijderoute reisde het mee met kooplieden en geleerden. In de 9e eeuw schreef een Perzische wiskundige, Muhammad ibn Musa al-Khwarizmi, een boek waarin hij dit nieuwe systeem uitlegde. Zijn werk was zo invloedrijk dat zijn naam ons het woord 'algoritme' gaf, en de titel van zijn boek, 'Al-Jabr', gaf ons het woord 'algebra'. Hij hielp mij en mijn held Nul te introduceren aan de Arabische wereld, en van daaruit veroverden we uiteindelijk Europa en de rest van de wereld.
Nu ben ik overal, en je denkt waarschijnlijk niet eens meer aan me. Ik zit in elke computer en elke smartphone. Computers spreken in binair, een taal die alleen uit nullen en enen bestaat. Zonder mij zouden die rijen nullen en enen betekenisloos zijn. Ik geef elke '1' zijn unieke kracht op basis van zijn positie, waardoor computers alles kunnen doen, van het spelen van je favoriete game tot het lanceren van een raket naar Mars. Ik help ingenieurs om wolkenkrabbers en bruggen te bouwen met uiterste precisie. Ik help wetenschappers de afstand tot verre sterrenstelsels te meten. Ik help bankiers om al het geld in de wereld bij te houden. Elke keer als je de score van een wedstrijd controleert, de tijd afleest op een digitale klok, of ingrediënten afweegt voor een recept, ben ik daar, stilletjes de wereld voor je aan het organiseren. Mijn verhaal is een herinnering dat zelfs de eenvoudigste ideeën, zoals een getal een eigen plek geven, de wereld volledig kunnen veranderen. Ik geef jou de kracht om te tellen, te bouwen, te dromen en het universum te begrijpen, één krachtige positie per keer.
Leesbegripsvragen
Klik om het antwoord te zien